In August 2007 I have decided to start in the Dutch Wikibooks a new book on classical mechanics, 'Klassieke Mechanica'. The last version of this book, version 1.14 of 2021-12-04, can be downloaded here in PDF-format. It has with text, table of content and index, 285 pages (4.4 MB). It has a clickable table of contents, references and index.
My first program was on relative motion. This topic was considered quite difficult by the students. After analyzing the problem I discovered that half of the knowledge used to solve this kind of problems was common sense knowledge, which was not explicitly mentioned in the course text. I then developed a program which showed clearly what kind of common sense knowledge is used and where. The program evolved through 4 different scripting languages, the last being Authorware. Text is in Dutch! Here is the program as a simple ZIP file, which will/should be unpacked in a separate directory. It runs on Windows XP and later. It runs also without problems under Linux with wine. Please read the leesmij32.txt file!
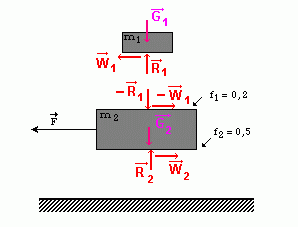
Another program was on how to apply the second law of Newton. This was first made in Phoenix, with four examples. I converted the main introduction to Authorware, but could not find the time to convert the examples. In Dutch! And same remarks as for the previous program.
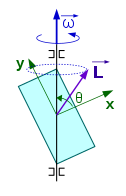
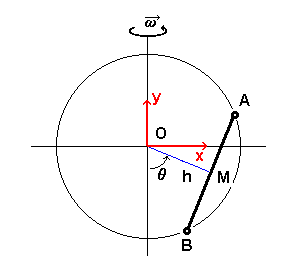
I also made a program on the behaviour of rotating objects (three dimensional rotation).It was first made in Linkway, a graphical DOS program made for IBM as a competitor for the Hypercard on the Apple. This was my first work in a program capable of supporting the VGA resolution (640x480 px!) and with linking as we know it now from websites. Recently (April 2020) I have completely reworked it in Authorware, as the other CAI programs. In Dutch!
There is a well know and quiet spectacular experiment about the conservation of angular momentum. It shows a person sitting in a chair, which can turn easily around its vertical axis, with a bicycle wheel in his hands. The wheel has a rim filled with lead to give it a greater moment of inertia. It's started spinning with the axis horizontal. When the man turns the axis vertical he starts himself and the wheel to turn in opposite sense of the spinning wheel, although nothing from outside has touched them.
Years ago I had several times discussions with people who pretended that the vectors used in physics are not
the same as in mathematics. They said that physics uses sliding vectors. This is nonsense. It means that physics should use some mathematics which do not belong to mathematics. The correct interpretation of this sliding vectors is that it is a form of using an equivalent description. The full theory is in the chapter "Equivalente vectorsystemen" in my text on Wikibooks. It's my conviction that letting a force vecor slide along its line of action should not be treated separately, as is almost always done, but that it should be understood as the simplest and oldest known form of passing on to an equivalent description. It's in this context that it receives its full meaning.
For many mathematicians it's a shock to hear that a translation is not a displacement along a straight line, but that a translation my follow any path. The only requirement is that orientation be kept, which means that what is horizontal should remain horizontal, what is vertical must remain vertical. There is a simple experiment which shows that both movements are completely different. It consists of a swinging bike wheel. The wheel can be allowed to turn freely around its axis and will then execute a translation, i.e. it will not rotate at all: the lower point (marked with green tape) will remain the lower point. One can also block the wheel with respect to the fork. Then it will execute a rotation as the orientation of the spokes changes continually. From the experiment results that a translating wheel gives an other period than a rotating wheel.
For a full explanation (in Dutch) see Wikibooks, Klassieke Mechanica, Dynamica van voorwerpen, rotatie versus translatie
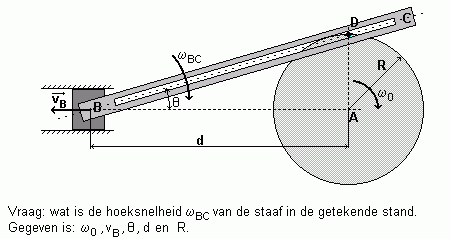
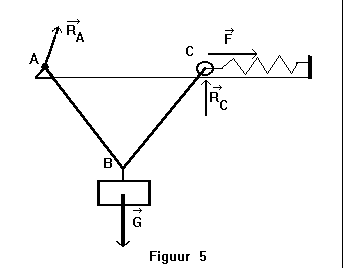
I also made a text where I describe four methods for calculating the dynamic equilibrium of the system shown in the picture below, each method being a bit simpler than the previous one. In Dutch.
My last text was on the method of virtual work. Already as a student I did not like the way this was presented. I finally made a presentation without imaginary or hypothetical elements and which does not treat differentials the way our grandfathers did. There is a presentation (in Dutch) of the theory (briefly!). A more elaborated text can be found in my text on Wikibooks (see top of this page).There is also the text of an article which represents the rationale behind the approach (in English).
In November 2005 I made a text on the evolution of spokes in bicycle and motorcycle wheels. This is one of the numerous stories where a seemingly good idea suddenly started giving problems when one thought to perfect the system. This text is intended for a broad audience, but is at this moment only in Dutch (pdf, 81 KB)
During 2006 I used the vast amount of pictures from the CAI programs on rotating objects for 2 articles in the Dutch Wikipedia, one about the simple case of rotation about an axis with a fixed orientation and one about the more complex general case. I felt that there were so many articles with partial information on these subjects, that a text covering the whole subject was really needed. But the texts where considered too long to be 'encyclopedic', and it was suggested that I should move them to the Dutch Wikibooks in a book on physics. Unfortunately this book was intended for youngsters of around 14 years, not precisely the public of my texts. So in August 2007 I have decided to start in the Dutch Wikibooks a new book on classical mechanics, 'Klassieke Mechanica'. I also made myself a PDF version of it with a clickable table of contents and index, which is not possible with the generator in Wikibooks. For more information and a link: see top of the page!
Last update: January 15, 2022